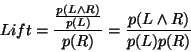CS579 Machine Learning: Assignment #1.
Due: at the beginning of the lecture on Thursday, January 27.
Assignment:Follow the instructions below.
Submit: your answers to
Exercises 1, 3, 4, 5 for the weather dataset,
Exercises 4, 5 for the census data, and Exercises 4, 5 for the
Market-basket data.
Learning Association Rules
For this assignment you will need to use Weka - Data Mining Software in Java.
You may download and install your own version of Weka (for Linux, Windows or Mac OS X) from this site:
http://www.cs.waikato.ac.nz/ml/weka/
.
You may also use Weka software (for Linux) which I installed in my directory
at
/home/faculty5/ipivkina/weka-3-4/
The site
http://www.cs.waikato.ac.nz/ml/weka/
provides a lot of information and
documentation on Weka.
Please use it.
In order to run, Weka needs Java to be installed. I installed a more
recent version of Java at
/home/faculty5/ipivkina/jdk1.5.0_01/bin/java
Feel free to use it.
To run Weka you may type
java -jar weka.jar
(add path to java and weka.jar in the above command if needed).
Weka software contains an implementation of the Apriori algorithm for
learning association rules.
Association rules are of the form LHS ==> RHS
where LHS and RHS are
sets of attribute-value pairs. These are called item sets: an
attribute-value pair is called an item.
For example:
rule 1 : outlook=sunny ==> play=no
rule 2 : temperature=cool windy=FALSE 2 ==> humidity=normal play=yes
Essentially, Apriori attempts to associate item
sets on the LHS with item sets on the RHS.
Weka's Apriori association rule algorithm
Apriori works with categorical values only. Therefore, if a dataset contains
numeric attributes, they need to be converted into nominal before
applying the Apriori algorithm.
For this part of the assignment we will use a
version of the weather dataset
weather.nominal.arff.
The datasets are in
weka-3-4/data directory
(in directory /home/faculty5/ipivkina/weka-3-4/data/ if you are using my
version).
Make sure you work with copies of the datasets if you are requested to
modify them.
Apply the Apriori algorithm to the nominal weather
dataset using Weka's command line interface (CLI).
java weka.associations.Apriori -t data/weather.nominal.arff
You should see output like the following:
Apriori
=======
Minimum support: 0.15
Minimum metric : 0.9
Number of cycles performed: 17
Generated sets of large itemsets:
Size of set of large itemsets L(1): 12
Size of set of large itemsets L(2): 47
Size of set of large itemsets L(3): 39
Size of set of large itemsets L(4): 6
Best rules found:
1. outlook=overcast 4 ==> play=yes 4 conf:(1)
2. temperature=cool 4 ==> humidity=normal 4 conf:(1)
3. humidity=normal windy=FALSE 4 ==> play=yes 4 conf:(1)
4. outlook=sunny play=no 3 ==> humidity=high 3 conf:(1)
5. outlook=sunny humidity=high 3 ==> play=no 3 conf:(1)
6. outlook=rainy play=yes 3 ==> windy=FALSE 3 conf:(1)
7. outlook=rainy windy=FALSE 3 ==> play=yes 3 conf:(1)
8. temperature=cool play=yes 3 ==> humidity=normal 3 conf:(1)
9. outlook=sunny temperature=hot 2 ==> humidity=high 2 conf:(1)
10. temperature=hot play=no 2 ==> outlook=sunny 2 conf:(1)
Description of Output
The default values for Number of rules, the decrease for
Minimum support (delta factor) and minimum Confidence
values are 10, 0.05 and 0.9.
Rule Support is the
proportion of examples covered by the LHS and RHS while
Confidence is the proportion of examples covered by the LHS
that are also covered by the RHS. So if a rule's RHS and LHS covers
50% of the cases then the rule has 0.5 support, if the LHS of a rule
covers 200 cases and of these the RHS covers 50 cases then the
confidence is 0.25.
With default settings Apriori tries to generate 10
rules by starting with a minimum support of 100%, iteratively
decreasing support by the delta factor until minimum non-zero support
is reached or the
required number of rules with at least minimum confidence has been
generated.
If we examine
Weka's output, a Minimum support of
0.15 indicates the minimum support reached in order to generate the 10
rules with the specified minimum metric, here confidence of 0.9.
The item set sizes generated are displayed; e.g. there are 6 four-item sets
having the required minimum support.
By
default rules are sorted by confidence and any ties are broken based
on support. The number preceding  indicates the number of cases
covered by the LHS and the value following the rule is the number of
cases covered by the RHS. The value in parenthesis is the rule's
confidence. These default settings can be modified using the
following options:
indicates the number of cases
covered by the LHS and the value following the rule is the number of
cases covered by the RHS. The value in parenthesis is the rule's
confidence. These default settings can be modified using the
following options:
|
-N | Specify required number of rules |
|
-C | Specify minimum confidence of a rule |
|
-D | Specify delta for decrease in minimum support |
|
-M | Specify lower bound for minimum support |
|
-I | if set the item sets found are also output (default = no) |
|
-T | sort examples by different metrics described below: |
| confidence (0) the default, Lift (1), Leverage
(2), Conviction (3)
|
Rules can be sorted according to different metrics. This is specified
using the -T option. Suppose we have the rule L 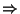 R and p(X) is the proportion of instances covered by the terms in
X. We shall express the various metrics using R, L and p.
R and p(X) is the proportion of instances covered by the terms in
X. We shall express the various metrics using R, L and p.
- Lift indicates the degree to which the rule improves the
accuracy of the default prediction of its RHS. Lift is confidence divided
by the proportion of all examples that are covered by the RHS;
i.e.
If the RHS covers 250 cases out of a dataset of 1000 then the Lift
is confidence/0.25.
- Leverage is the proportion of additional examples
covered by both the LHS and RHS
above those expected if the LHS and RHS were independent of each
other; i.e.
For example, suppose that there are 1000 examples, the LHS covers 200
examples, the RHS covers 100 examples, and the RHS covers 50 of the
examples covered by the LHS. The proportion of examples covered by
both the LHS and RHS is 50/1000 = 0.05. The proportion of examples
that would be expected to be covered by both the LHS and RHS if they
were independent of each other is (200/1000) * (100/1000) = 0.02.
Leverage = 0.05 - 0.02 = 0.03. The total number of examples that
this represents is 30.
- Conviction is similar to Lift but considers the effect
when the RHS is not true, and the ratio is inverted.
In the above example p(L) is 200/1000,
p(not R) is 900/1000, and p(L 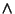 not R)=150/1000.
Thus Conviction is 0.2*0.9/0.15 = 1.2.
not R)=150/1000.
Thus Conviction is 0.2*0.9/0.15 = 1.2.
Exercises
- How might you change the dataset before an item set of 5 can be
generated?
- Set (-I yes) to view details of generated item sets.
- How might you change the values for -N, -C, -D and -M to increase the number of generated rules?
- Using the default value for -N, -D and
-C, identify the maximum value for -M that would enable
at least one rule to qualify (when sorted by confidence).
- Specify different values for -T and
compare rule rankings by Confidence, Lift and Leverage.
Are the top ranking rules affected by different -T values?
Exercises with census data
We will now use the adult.arff
dataset which contains census data collected from about 48842 US adults.
The goal of this dataset is to predict whether income exceeds $50000,
however for association rule learning this is irrelevant.
The original dataset is taken from the UCI Machine Learning Repository.
More information about it is available in the original UCI Documentation
http://www.ics.uci.edu/~mlearn/MLRepository.html.
Attributes 3 and 5 in this dataset are numeric, therefore before
applying the Apriori algorithm you will need to preprocess this
dataset using the Discretize Filter in order to create a dataset with
just nominal attributes.
You may do it by typing the following (specify paths for java, adult.arff and adult-disc.arff if needed):
java weka.filters.unsupervised.attribute.Discretize -R 3,5 -B 10 -i adult.arff -o adult-disc.arff
Here -R specifies list of attributes to Discretize,
-B specifies the (maximum) number of bins to divide numeric attributes into.
The new file will be saved in
adult-disc.arff
with attributes 3 and 5 converted into nominal.
(More information on
Class Discretize
you may find in the
Weka API documentation.)
Generate association rules for the discretised Adult dataset.
Repeat the same exercises carried out with the nominal weather dataset
by trying out different option values and sorting metrics.
Exercises with Market-basket data
In this part we will use
market-basket.arff dataset.
- Load this into a text editor and analyze the attribute types and
values.
- What kind of application might have given rise to these instances?
- Convert the dataset into a format that is suitable for Weka's
Apriori algorithm (tip: use a bin size of 3 when discretizing).
- Apply the algorithm using the CLI and analyze the rules
generated with different options.
- Use Weka's GUI (Explorer interface) to launch the Apriori
algorithm by clicking on the association tab (use the preprocess tab
to load your dataset).