Part 1 Do the following exercises from the textbook.
3.8a-d, 3.18
Part 2 Goat, Cabbage and Wolf problem is defined as follows. A farmer and his goat, wolf, and cabbage come to a river that they wish to cross. Besides the farmer himself, the boat allows him to carry only one of them at a time. Without supervision, the goat will gobble the cabbage whereas the wolf will not hesitate to feast on the goat. Find a sequence of crossing to transport safely all of them across the river.
(a)
Formulate this problem as a state-space search problem
Give a precise definition of a state, the start state, the goal state or
goal condition, the operators, and the path cost.
(b)
Show the State Space
Draw the complete state-space graph that includes all nodes (and legal
directed arcs connecting these nodes)
for this problem. Inside each node show the state description.
(c) Draw a search tree for this problem up to depth 5.
(d) Find a solution to the problem (it may have depth more than 5).
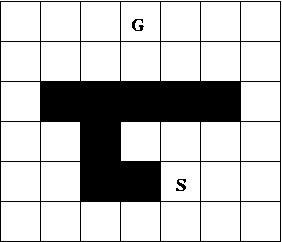
Part 3 Comparing Multiple Search Methods Consider the problem of finding a path in the grid shown below from starting square S to goal square G. Possible moves from a square are to move left, up, right, and down exactly one square. No move may be made onto a dark square (i.e., obstacles) or off the edge of the grid.

(a) Depth-First Search
Copy the grid and then mark the grid squares with the number(s) indicating when
that square is expanded during a Depth-First search from S to G. Assume
children nodes are visited in the order left, up, right, down. Assume cycle
checking is done so that a node is not generated in the search tree if the
grid square position associated with the node occurs somewhere on the path
from this node back to the root node.
Highlight the solution path found, if any,
or explain why none is found.
(b) Greedy Best-First Search
Copy the grid again and then mark the grid squares with the number(s) indicating
when that square is expanded during a Greedy Best-First search from
S to G. Use as the heuristic function
h(n) = |xn - xg| + |yn - yg|
where the grid square associated with node n is at coordinates
(xn, yn) in the
grid and the goal node G is at coordinates
(xg, yg). Assume you do not generate a
node if that node's associated grid position has previously been generated.
In the case of ties in evaluation function values, for siblings expand
them in the precedence order left, up, right, down. In the case of ties
between non-siblings, use FIFO order to expand first the node that has been
in the NODES list the longest.
Highlight the solution path found, if any, or explain why none is found.
(c) A* Search
Copy the grid again and do the same as in (b) except using A* search
with the same heuristic function as in (b) and the cost of each move equal to 1.
Use the same tie-breaking rules as defined in (b).
Highlight the solution path found, if any, or explain why none is found.
(d) Hill-Climbing (Gradient descent) Search
Copy the grid again and use Hill-Climbing (Gradient descent) Search.
As above, number the squares
when a node is expanded. Use the heuristic function defined in (b).
Use the same tie-breaking rules as defined in (b).
Highlight the solution path found, if any, or explain why none is found.
(e) An Infinite Grid
Suppose the grid is extended infinitely in all directions but S, G and
the dark squares remain as before. Which of the following methods will
not be able to find a solution to this problem? Breadth-First, Depth-First,
Depth-First Iterative Deepening, Greedy Best-First, and A*.
Which of these would be the best method, and why?
Again, in the case of ties in ordering nodes on the NODES list,
use the precedence defined in (b).